January 1, 2024

An Accessible Introduction to Abstract Argumentation Frameworks

With his paper [1] in 1995, Dung laid the foundation for the abstract argumentation framework and with it one of the widely studied argumentation systems. This is not without reason, as the simplicity of the framework makes it a good starting point for further investigations and additions. An abstract argumentation framework (AF for short) consists of arguments (the statements) together with the attack relations between these arguments. However the internal structure of an argument is insignificant and is the cornerstone of abstractness.

An abstract argumentation framework (AF) is a pair ⟨Arg, AR⟩, where
Arg is a set of arguments and AR ⊆ Arg × Arg is a binary relation.

In order to extract the arguments to be accepted in such an abstract argumentation system, the conflicts are resolved on a semantic level. Semantics, a function that selects a subset of arguments based on certain criteria, is used for this purpose.

Specification of the Running Example

In the following, we will familiarise ourselves with the concept of the argumentation frameworks using the following basic example:

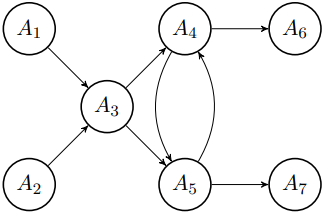
An image depicting an argumentation framework containing 7 arguments and their attack relation — The argumentation framework used as a running example in this blog post.

The argumentation framework comprises seven distinct arguments, denoted by A_iwhere i is an index. While the internal details and meanings of the arguments are not relevant for working with the framework, defining them can aid in understanding the concept:

A₁: There are no good movies in the cinema programme
A₂: The cinema is closed today
A₃: We should watch a movie tonight
A₄: Today is saturday
A₅: There is free entrance to museums today
A₆: We are going to visit the computer museum
A₇: On saturday we play a board game

With the definition given earlier, we can describe this AF as follows:

F = ({A₁,A₂,A₃,A₄,A₅,A₆,A₇},{(A₁,A₃),(A₂,A₃),(A₃,A₄),(A₃,A₅),(A₄,A₅),(A₅,A₄),(A₄,A₆),(A₅,A₇)})

The Properties of Conflict-Freeness and Admissibility

To find algorithms for identifying jointly accepted arguments, we first need to take a closer look at two properties. These two basic properties are conflict-freeness and admissibility. Conflict-freeness arises when there is no attack relationship between the arguments for two arguments in the subset S. The set S is a proper subset of all arguments in an argumentation framework, i.e. S ⊆ Arg. In the running example, these are all the sets of arguments A₁ to A₇ that can be formed. For example: {A₁,A₂}, {A₄,A₇} or even the empty set {}.

A subset S is therefore conflict-free if all the sets of arguments it contains have no conflict with each other.

A set S of arguments is conflict-free if no argument in S attacks an argument in S.

Applying this definition to all possible subsets, we can make out a lot of conflict-free sets for our running example. Therefore, we inspect only a few examples. First of all, the empty set {} always falls under this definition. Another intuitive conflict-free set would be {The cinema is closed today, Today is saturday}, i.e. {A₂,A₄}. However, also sets like {We should watch a movie tonight, We are going to visit the computer museum}, i.e. {A₃,A₆}, are conflict-free. This is because between those two arguments there is no attack relation and therefore they fall under the definition of conflict-freeness.

To eliminate sets where arguments could be not accepted due to being attacked by another argument of the argumentation framework, a more restrictive property is needed, namely admissibility. Admissibility is given for a conflict-free subset S if every argument in the subset is defended by the arguments in the subset S. Defence is defined by the fact that an argument a is always defended by the subset S if for every attacker b on a there is a defender c that exists b.

An argument a ∈ Arg is defended by a set S ⊆ Arg if, for each b ∈ Arg such that (b, a) ∈ AR, there exists c ∈ S such that (c, b) ∈ AR.
The characteristic function Γ_F(S) is a function that returns all arguments that are defended by the extension S, i.e. Γ_F(S) = {a ∈ Arg ∣ S defends a}.

An set of arguments S is admissible if S is conflict-free and each argument
is defended by S such that S ⊆ Γ_F(S).

With the admissibility property, we can therefore exclude sets such as {We should watch a movie tonight, We are going to visit the computer museum}, i.e. {A₃,A₆}, in our running example. Here A₃ is attacked by A₁ and A₂, but not defended by any argument from {A₃,A₆}. In contrast, sets like {A₂,A₄} remain as desired.

The Classical Semantics

In the following, we take a look at the semantics originally proposed by Dung. These are often referred to as the classical semantics. Although the two properties conflict-freeness and admissibility are not ordinarily semantics, they are often counted among them for reasons of simplicity. In addition, many other semantics have been discovered in the almost three decades since Dung's initial work.

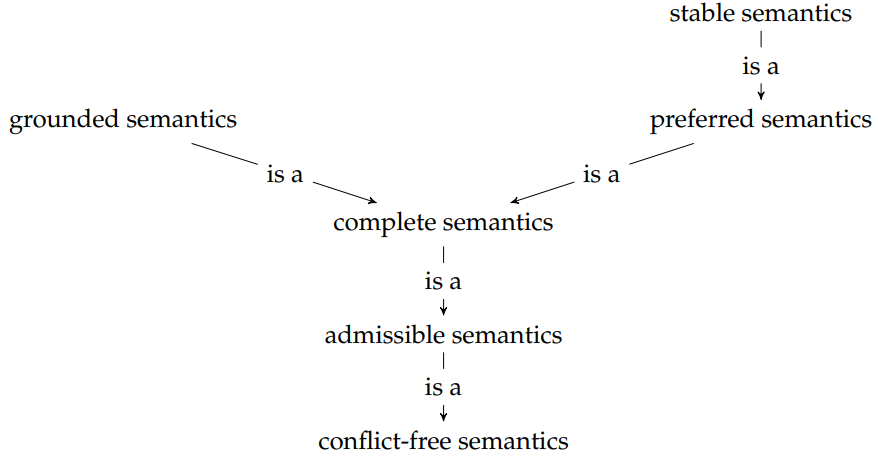
A semantics is a function that takes an argumentation framework and applies certian conditions such that a set of extensions is produced. An extension contains only the arguments which can stand together according to these conditions. A semantics function ranges from having no extensions at all and a multitute of extensions.

For a given set S, if S ∈ σ(F), then S is called a σ-extension, i.e., an extension under the semantics σ.

Complete Semantics

The complete semantics is the foundation for all other classical semantics. The extensions of this semantics are characterised by being admissible but also defending themselves and also including all the defended arguments. The last condition sets the complete semantics apart from the property of admissibility.

A set of arguments E ⊆ Arg is a complete extension if E is admissible and Γ_F(E) = E.

From the given definition it is easy to see the difference between admissibility and the complete semantics. While the former demands that a given set is just a subset of the characteristic function, the latter states that the given set must be equal to the characteristic function. Remember that the characteristic function for a set given returns all the defended arguments by this set.

If we now apply this semantics to our current example, we obtain the following three extensions: {A₁,A₂}, {A₁,A₂,A₅,A₆} and {A₁,A₂,A₇,A₄} which translate to:

{There are no good movies in the cinema programme, The cinema is closed today}
{There are no good movies in the cinema programme, The cinema is closed today, There is free entrance to museums today, We are going to visit the computer museum}
{There are no good movies in the cinema programme, The cinema is closed today, Today is saturday, On saturday we play a board game}

All three extensions now only contain arguments that also hold up as a conclusion from a human perspective. The two extensions with 4 arguments are the result of a decision in favour of argument A₄ or A₅, as both are in conflict with each other.

Grounded Semantics

The grounded semantics determines a unique extension. There is always only exactly one grounded extension. It is equal to the complete extension that contains the least amount of defended arguments, but is still defending itself.

There are two ways to express the grounded semantics. For a set of arguments E ⊆ Arg is a grounded extension if and only if
A) E is admissible and E is the minimal complete extension with respect to set inclusion.
B) E is the least fixed point of the characteristic function Γ_F(E).

The only grounded extension in the current example is {A₁,A₂} and thus {There are no good movies in the cinema programme, The cinema is closed today}. This also makes the intention behind the grounded semantics clear: it contains the complete extension that does not require a decision. The arguments can therefore stand for themselves.

Preferred Semantics

The preferred semantics is a stricter than the complete semantics. The general idea is that it finds all those extensions that can defend themselves and are as large as possible.

A set of arguments E ⊆ Arg is a preferred extension if and only if E is admissible and E is a maximal admissible set with respect to set inclusion.

The intuition can be recognised from our running example. If we look at the complex extensions, there are three of them, one of which is identical to the grounded extension. To put it loosely, this extension does not contain any decisions. With preferred semantics, on the other hand, we want to find all extensions for which a decision has been made. It is therefore not surprising that {A₁,A₂,A₅,A₆} and {A₁,A₂,A₇,A₄} are the preferred extensions. It is also easy to recognise that there is no complete superset of them:

{There are no good movies in the cinema programme, The cinema is closed today, There is free entrance to museums today, We are going to visit the computer museum}
{There are no good movies in the cinema programme, The cinema is closed today, Today is saturday, On saturday we play a board game}

Highlighted representation of both preferred extensions in the running example.

Stable Semantics

The last classical semantics is the stable semantics. It builds on the preferred semantics and its extensions follow the concept that all arguments that are not in a stable extension should be attacked by the extensions. This is a rather radical requirement and therefore the stable semantics sometimes produces no extensions at all for a given argumentation framework.

A set of arguments E ⊆ Arg is a stable extension, if and only if E is complete and for every arguments a ∈ Arg \ E, an argument of E attacks a.

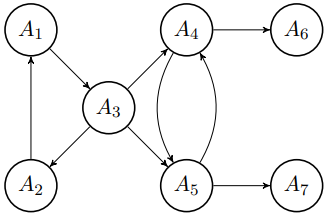
A modification of the running example to show odd cycles and their influence on the stable extensions.

For our running example, the stable extensions are identical to the preferred ones. This is because the sets {A₁,A₂,A₅,A₆} and {A₁,A₂,A₇,A₄} attack all other arguments. But what if argument A₂ (The cinema is closed today) attacks argument A₁ (There are no good movies in the cinema programme)? In this case, an odd cycle occurs between A₁, A₃ and A₂. In this case, there is no stable extension, since the only complete extension is the empty set {}. And as the empty set has no arguments, it therefore cannot attack any. According to the stable semantics, there can consequently be no extension.

Highlight of the odd cycle of the modified AF.